FUNÇÃO DO 2º GRAU

FUNÇÃO DO 2º GRAU


DEFINIÇÃO

Chama-se função quarática a função definida por:

Y = ax² + bx + c

onde a, b e c são números reais e a ≠ 0.

Exemplos:

1) Y = x² - 7x + 10

2) Y = 3x² - x – 4

3) Y = 3x²

4) Y = x² - 4

EXERCÍCIOS

1) Quais são funções quadráticas?

a) Y = x² - 5x + 6 (X)

b) Y = 3x² - 2x + 1 (X)

c) Y =n 5x – x + 3

d) Y = 2 + 4x – 1

e) Y = 5x² (X)

f) Y = -x² + 4 (X)

g) Y = 2x – 5

h) Y= x²/3 – 4x (X)

2) Verifique se a funçao Y = (2x – 1)² - 4 ( x+1)² é uma função quadratica. 
(R: não)

3) Obter m na função Y = ( m + 2)x² - 5x + 1 para que seja quadrática
R: m + 2 ≠ 0 e m≠-2



REPRESENTAÇÃO GRÁFICA DA FUNÇÃO DO 2º GRAU



Vamos atribuir a x valores quaisquer do conjunto dos números reais e calcular o correspondente de y .
O gráfico da função quadrática, quando definida de R em R, é uma curva denominada parábola, como nos seguintes exemplos:

1) Seja a funão definida por: y = x² -4x + 3
Solução :

Vamos atribuir a x os valores : -1,0,1,2,3,4 e 5 e calcular os valores de y.


















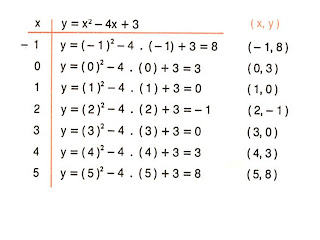
a seguir:

1º) Marcamos os pontos no gráfico.
2º) Traçarmos a curva

Os ponto V indicado na figura chama-se vértice da parabola


2) Seja a função definida por: Y = -x² -6x - 8

Solução:

Vamos atribuir a x os valores 0,1,2,3,4,5 e 6 e calcular o valor de y
















A seguir
1º) Marcamos os pontos do gráfico.
2º) Traçamos a curva

O ponto V indicado na figura é o vértice da parábola

3) Seja a função definida por : Y = x² -2x + 1

Solução:

Atribuindo-se valores para x obteremos valores correspondentes para y.

veja:

A seguir :

1º) Marcamos os pontos no gráfico.
2º) Traçamos a curva

O ponto V indicado na figura é o vértice da parábola

CARACTERÍSTICAS DA FUNÇÃO QUADRÁTICA

a) Quando à concavidade da parábola:

















b) Quanto às coordenadas do vértice:

EXERCÍCIOS

1) Observe cada função quadrática e responda se o gráfico da parábola tem concavidade para cima ou para baixo,

6) Dada a função y = x²+ 2x+ 2 complete a tabela e esboce o seu gráfico:

a) y= x²-3x + 2

b) y= x² + 4x -3

c) y = x²-4x +4

d) y = -x² + 6x – 9

e) Y = x² - x + 2

f) y = x² - 4

g) y = -x² + 9

h) y = x² - 3x

i) y = x² - 2x – 8

j) y = 2x²

ZEROS DA FUNÇÃO QUADRATICA

Os zeros da função quadrática y = ax² + bx + c, são os valores de x para os quais y = 0

Então:

Achar os zeros da função quadrática equivale a resolver a equação do 2º grau

ax² + bx + c = 0 ( a diferente de 0)

EXEMPLOS

Dada a função x² - 5x + 6:

a) Obtenha os zeros da função

b) Com os zeros obtidos esboce o gráfico da função

Os zeros da função são 2 e 3.

2) Dada a função y = -x² + 6x – 9:

a) Obtenha os zeros da função.

b) Com os zeros obtidos esboce o gráfico da função.

3) Dada a função y = x² -2x + 5:

  
               a) Obtenha os zeros da função.

b) Com os zeros obtidos esboce o gráfico da função.

EXERCÍCIOS